Ex 33, 1 Solve the following pair of linear equations by the substitution method (vi) 3𝑥/2−5𝑦/3=−2 𝑥/3𝑦/2=13/6 Removing fractions from both equations 𝟑𝒙/𝟐−𝟓𝒚/𝟑=−2 Multiplying both equations by 6 6 × 3𝑥/2−"6 ×" 5𝑦/3="6 ×"−2 9x – 10y = − 12EduRev Class 10 Question is disucussed on EduRev Study Group bySolve the following pair of linear equations by the substitution method (3x)/2 (5y)/3 = 2, x/yy/2 = 13/6

4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
X-y=3 x/3 y/2=6 by substitution method
X-y=3 x/3 y/2=6 by substitution method-Solve equations using substitution method 2 x − y = 3 and 4 x y = 3 A Click here 👆 to get an answer to your question ️ 3x/25y/3=2;x/3y/2=13/6 in substitution method




3 Y 9 Buy Clothes Shoes Online
Solving Systems Of Equations By Substitution Method In this method, we first find the value of one variable (y) in terms of another variable (x) from one equation Substitute this value of y in the second equation Second equation becomes a linear equation in x only and it can be solved for x Putting theIn this page substitution method questions 2 we are going to see solution of first question in the worksheet of substitution method What is substitution method ?Solve the following pair of linear equations by the substitution method (i) x y = 1 4 (ii) s − t = 3 x − y = 4 3 s 2 t = 6
Solve the following systems of equations 2/x 3/y = 9/xy 4/x 9/y = 21/xy, where, x ≠ 0, y ≠ 0 asked Apr 26 in Statistics by Haifa ( 521k points) pair of linear equations in two variablesSolve by Substitution y=x6 y=2x3 y = x 6 y = x 6 y = −2x − 3 y = 2 x 3 Eliminate the equal sides of each equation and combine x6 = −2x−3 x 6 = 2 x 3 Solve x6 = −2x−3 x 6 = 2 x 3 for x x Tap for more steps Move all terms containing x x9x 3y = 9 (iv) 02x 03y = 13 ;
For example, in part (iv) it is most convenient to substitute the value of x from the first equation to the second equation, as the division by 02 is more easier than the division by 03, 04 and 05 Question 2 Solve 2x 3y = 11 and 2x – 4y = – 24 and hence find the value of 'm' for which y =mx 3In this section, you will learn how to solve system of equations using substitution method Solving Systems of Equations Using Substitution Procedure (a) Use one of the equations in the system of equations to solve for one of the variables in terms of the other variables y = (3 2√3)/6 x = 2 x 3 = 2x This is an equation involving x alone, and we can solve it as usual x 3 = 2x → 3 = 2x − x → 3 = x Once we find one variable, we deduce the other using it's explicit representation we knew that y = x 3, and now we know that x = 2 Thus, y = 3 3 = 6 PS, note that this was a special case, since both equations were an




Graph Graph Inequalities With Step By Step Math Problem Solver




Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Video Online Download
OSMBOY OSMBOY Math Secondary School answered X/22y/3=1 and xy/3=3 solve by elimination method 2 See answers Advertisement Advertisement KrishnaPolavarapu KrishnaPolavarapu Here's your answer Hope it was helpful AdvertisementX y = 4 (ii) s t = 3;2(62y)3y=8 124y3y=8 12y=8 y=128 y=4 #3 3xy=1 x=2y5 sol let, 3xy=1 eq(i) x=2y5 eq(ii) substitute the value of x from eq(ii) in eq(i), then eq(i)will be 3(2y5)y=1 6y15y=1 7y15=1 7y=115 7y=14 y=2 #4 xy=6 y=32x sol let, xy=6 eq(i) y=32x eq(ii) substitute the value of y from eq(ii) in eq(i) then eq(i) will be x(32x




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula



Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf
√(3)x √(8)y = 0 (vi) 3x2 5y3 = 2 Answers fast please 1) y=x−63x2y=8 Use the substitution method A) (4, −2) B) (14, 8) C) (0, −6) D) (3, −3) 2) What is the xcoordinate of the(x, y) = (1, 1) After having gone through the stuff given above, we hope that the students would have understood, how to solve system of linear equations by substitution method Apart from the stuff given in this section, if you need any other stuff in
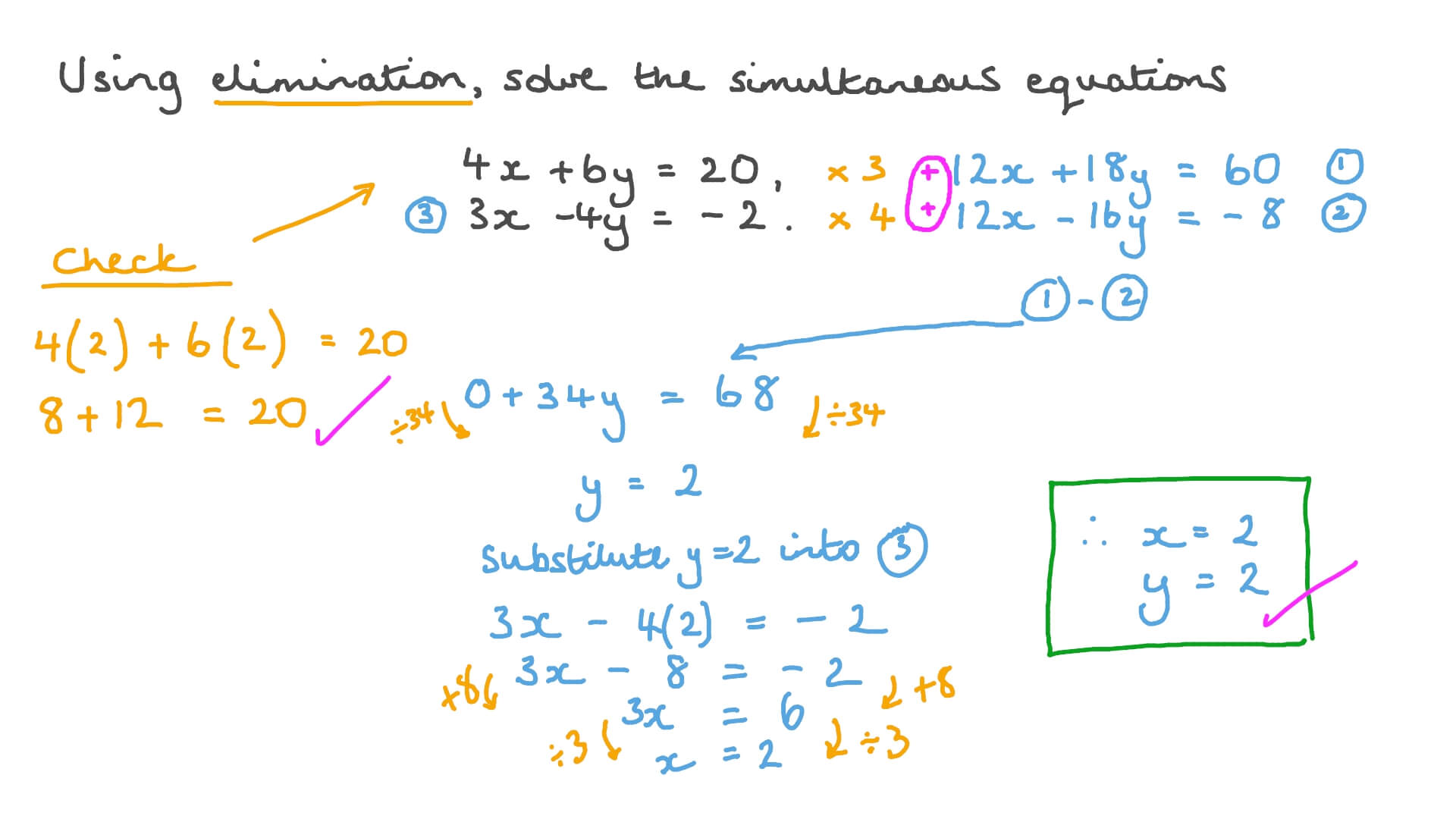



Question Video Solving Simultaneous Using Elimination Where Both Of The Equations Needs To Be Multiplied Nagwa




Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Updated For 21 22 Coolgyan Org
Substitution Method – Example Study the example below that shows how to use the substitution method in systems of equations Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label the equations Label the equations A and B (A) 3x 2y = 4 (B) x 4y = 3 Step 2 Isolate one of the variables`= x = 42/3 = 14` Hence, the solution of thee given system of equations is x = 14, y = 9 Concept Algebraic Methods of Solving a Pair of Linear Equations Substitution MethodSolve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submit



Web Gccaz Edu Johwd Mat150 Chapter8 Solutions Section 8 1 solutions Pdf




Chapter 5 Review Exercises
Aubrey is using the substitution method to solve the following system of equations y − x = 21 2y = 2x 16 She arrives at an answer of 8 = 21 She thinks that this answer means that the lines are parallel and that the system has no solution04x 05y = 23 (v) √(2)x √(3)y = 0 ; Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2 29y = 19 y




Solution Of X Y 3 And X 3 Y 2 6 By Elimination Method Brainly In




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution
Solve the following system of equations 2/x 3/y = 9/xy 4/x 9/y = 21/xy asked in Linear Equations by ShasiRaj ( 625k points) pair of linear equations in two variablesClick here👆to get an answer to your question ️ Solve the following pair of linear equations by the substitution method 3x y = 3 9x 3y = 9How do you solve #xy=5# and #3xy=15# using the substitution method?




2x 3y 12 X Y 1 Simultaneous Equation Graphically 2x 3y 12 X Y 1 Simultaneous Equation Graphically Josspixqaak



How To Solve This System Of Equations 3x 5y 6 2x 3y 4 Quora
Substitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm1440 votes 1 answer Which method do you use to solve the system of equations #y=1/4x14# and #y=19/8x7#?




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic




Homework Pencil Red Pen Highlighter Notebook Calculator Answer
Solve each of the following systems of equations by the method of cross multiplication 2/x 3/y = 13 5/x 4/y = 2 where x ≠ 0 and y ≠ 0 asked Apr 27 in Linear Equations by Gargi01 (506k points) pair of linear equations in two variables;Click here👆to get an answer to your question ️ Solve the following pair of linear equations by the substitution method(i) x y = 14; , x/2 y/2=13/6?ans x=2,y=3?




7x 3y 1 0



2 2solve Using Substitution M See How To Solve It At Qanda
Let's start by clearing those fractions The LCD for the first equation is 6, for the second equation is 15, so multiply both sides of these equations by those numbersSteps for Solving Linear Equation y=2x3 y = −2x − 3 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2x3=y −2x − 3 = y Add 3 to both sides Add 3 to both sides X/22y/3=1 and xy/3=3 solve by elimination method Get the answers you need, now!




Solve The Pair Of Linear Equations By Substitution 3x 2 5y 3 2
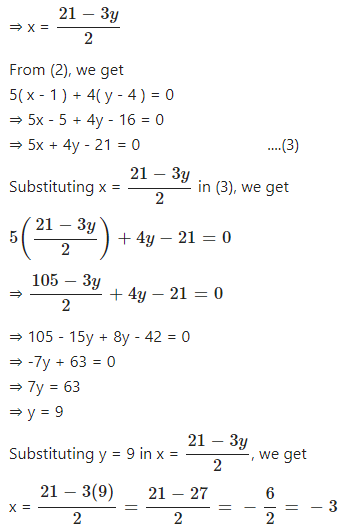



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp
Question 4841 Solve the system by the addition method x/3y/2=5/6 x/5y/3=3/5 Answer by rapaljer (4671) ( Show Source ) You can put this solution on YOUR website! x = 1 and y = 4 Another method which will work well in this case is to equate two equal expressions This is a form of substitution Transpose both equations to give y = equ 1 y = x 3" and " equ 2 y = 7x 3 Note that " " y = y Therefore 7x 3 = x 3 " " 6x = 6 " "x = 1 Equ 1 y = 1 3 rArr y = 4The following steps will be useful to solve system of linear equations using method of substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3




7x 3y 1 0




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo
Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 If the answer is not available please wait for a while and a community member will probably answer this soonSolve the following pairs of linear equations by the substitution method 3x/2 5y/3 = 2, x/3 y/2 = 13/6What are the 2 numbers if the sum is 70 and they differ by 11?




Ncert Solutions Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ship Hang Nhanh



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero
Aug 23,21 Solve these linear equations by substitution method 3x/2 5y/3 =2 x/3 y/2 =13/6?Solve the Given equation in Elimination method and Substitution MethodS3 t2 = 6 (iii) 3x y = 3 ;




4 Given F X And G X Find F G X 5 8 X Chegg Com



Double Integrals Over General Regions Calculus Volume 3
Solve for x x in the first equation Tap for more steps Move all terms not containing x x to the right side of the equation Tap for more steps Add 1 1 to both sides of the equation Add 3 3 and 1 1 Divide each term by 2 2 and simplify Tap for more steps Divide each term in 2 x = 4 2 x = 4 by 2 2Solve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6Solve by Substitution 2xy=6 , xy=3 2x − y = 6 2 x y = 6 , x y = −3 x y = 3 Subtract y y from both sides of the equation x = −3 −y x = 3 y 2x−y = 6 2 x y = 6 Replace all occurrences of x x with −3−y 3 y in each equation Tap for more steps




X Y 3 And X 3 Y 2 6 Solve The Following Pair Of Linear Equations By The Elimination Method And Brainly In




Solving Systems Of Equations With Fractions Or Decimals Video Lessons Examples And Solutions
Correct answer xy=3 and X/3 y/2 = 6 Solve the following pair of linear equations by the elimination method and the substitution method eanswersincomExample 1 Solve the following pair of linear equations by the substitution method 02x 03y = 13 and 04x 05y = 23 Solution 02 x 03 y = 13 (1)Solving system of equation by substitution method, involves solving any one of the given equation for either 'x' or 'y' and plugging that in the other equation and solve that equation for another variable



The Substitution Method




Solved Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0
Cancel the common factor Divide y y by 1 1 Divide 3 3 by 3 3 Replace all occurrences of y y with 1 1 in each equation Tap for more steps Replace all occurrences of y y in x = y x = y with 1 1 Remove parentheses The solution to the system is the




X Y 3 X 3 Y 2 6 Youtube




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com



Http Www Standrewspaisley Com Uploads 6 0 2 3 Circle Pupil Booklet Pdf



Solve For X And Y X 2 2y 3 1 X Y 3 3 Sarthaks Econnect Largest Online Education Community




3 Y 9 Buy Clothes Shoes Online



Www Keble Ox Ac Uk Wp Content Uploads Ch 1 Algebra Pdf




6 X Y 7 X Y 3 1 2 X Y 1 3 X Y




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In




3 Systems Of Linear Equations




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube




Solve The Following Pair Of L See How To Solve It At Qanda



Systems Of Linear Equations
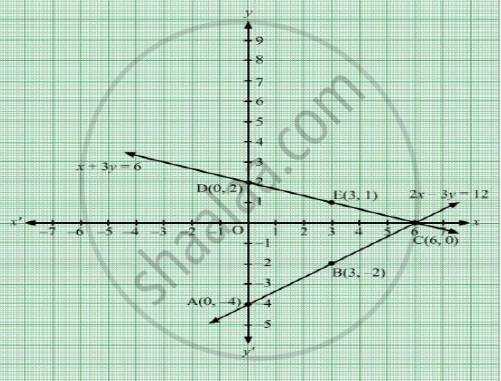



Solve Graphically The System Of Equations 2x 3y 12 X 3y 6 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The Y Axis Mathematics Shaalaa Com




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Solve The System Using Gaussian Elimination Or Gauss Jordan Elimination 3x 3y 3z 30 9x 9y 9z 90 1 5x 1 5y 1 5z 15 Select One A 2 2 6 Ob X Y Z 1 3x 3y 3z 30 Os Solve The



How To Solve The Simultaneous Equations X 2 Y 2 36 And X 2y 6 Quora



Onlinelibrary Wiley Com Doi Pdf 10 1002 Oth2




Find The Value Of X And Y X 3 Y 4 11 5x 6 Y 3 7 By Substitution Method Maths Meritnation Com



X 2 2y 3 1 And X Y 3 3 By Elimination Method And Substitution Method




Systems Of Equations And Matricies




Systems Of Equations Substitution Method Ppt Video Online Download



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic



How To Transform The Linear Equations X Y Z 6 2x Y 2z 10 3x 3y 4z 21 In A Matrix Equation And Solve Them By Finding The Inverse Of Coefficient Matrix Using The Adjoint Method Quora




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In



Http Palmer Wellesley Edu Ivolic Pdf Classes Handouts Algebraprecalcreview Review Factoring
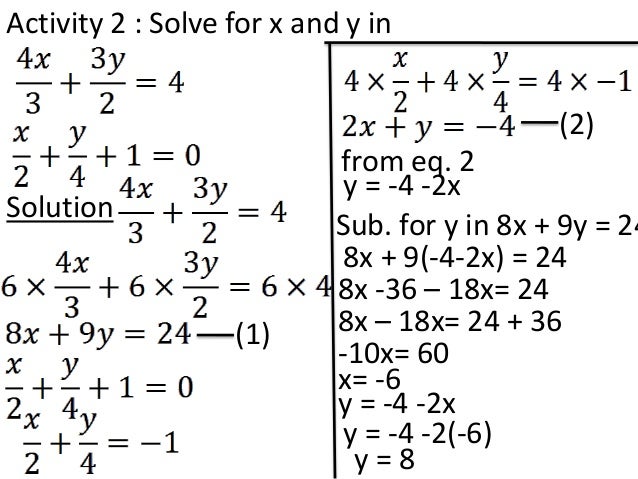



Simultaneous Equations




Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




7 Solve The System Of Equations Ii X 3 Y 2 X Y Homeworklib



Http Www Livingston Org Cms Lib9 Nj Centricity Domain 937 Summer warm up answer key Pdf



The Substitution Method
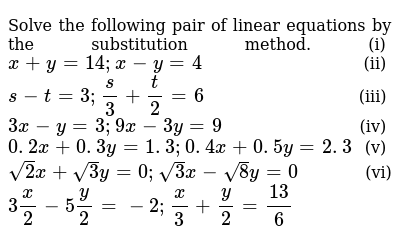



Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6




Ionic Transport Properties Of La X Y 3 X Fe 5 O 12 D Compounds A The Download Scientific Diagram




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Solved Exercise 3 3 Ve The Following Pair Of Linear Equations By The Substitution Method 1 Solve The Following X Y 14 Us T 3 St X Y 4 Ii 3x Y Do 9x 3y 9 3 5 6 Iv 0 2x 0 3y 1 3




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables



The Substitution Method




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution



Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria



Http Www Math Wsu Edu Students Odykhovychnyi M1 04 Ch04 All Pdf




14 2 Limits And Continuity




Exercise 3 3 1 Solve The Following Pair Of Linear Equations By The Substitution Method 0 X Y 14 I S 1 3 S 6 X Y 4 Ii 3x Y 3 9x 3y 9 V 0 2x 0 3y 13 0 4x 0 5y 23 12x 13




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube



Graph Graph Inequalities With Step By Step Math Problem Solver




Graph Graph Inequalities With Step By Step Math Problem Solver



Simultaneous Equations Gmat Math Study Guide



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video




Solve The System Of Equations Using Substitution Y 4x 6 Y 2x




Solve The Following Pair Of L See How To Solve It At Qanda




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
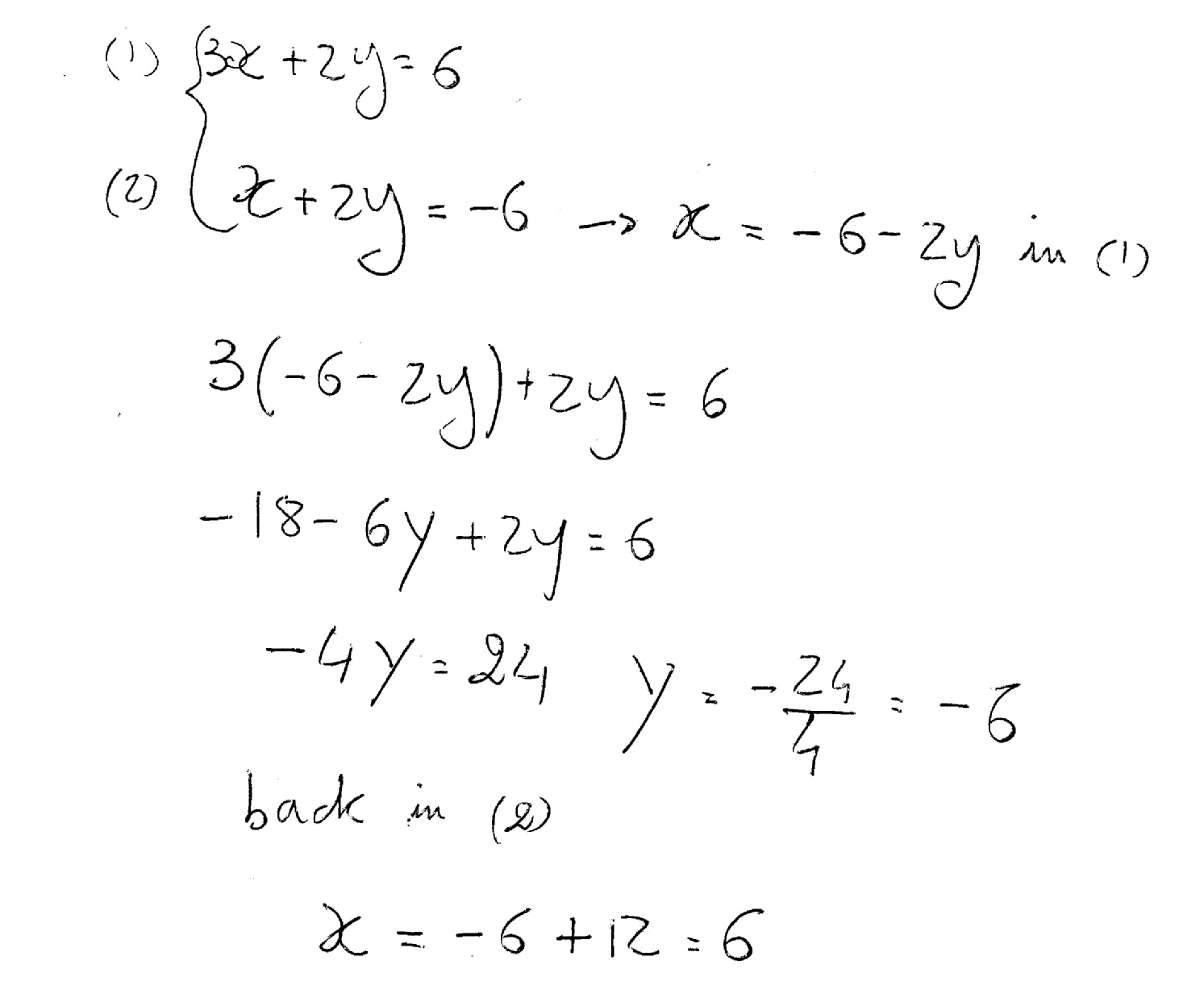



How Do You Solve By Substitution 3x 2y 6 And X 2y 6 Socratic
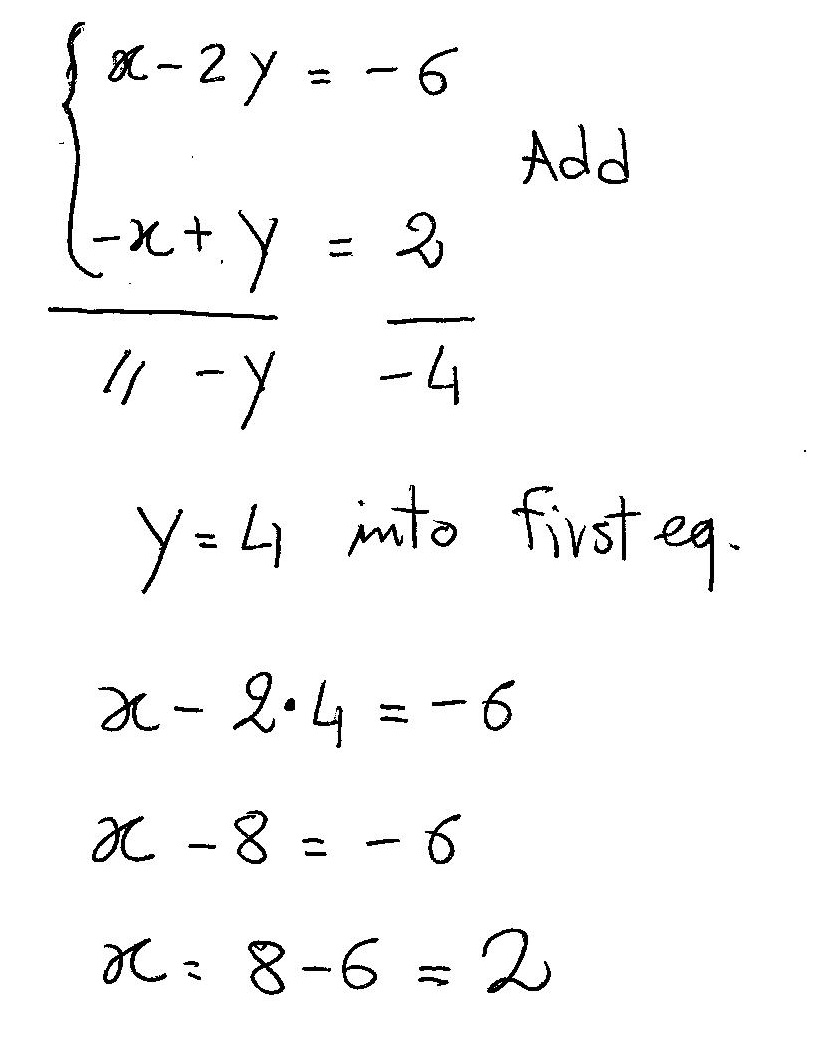



How Do You Solve X 2y 6 And X Y 2 Socratic




1 Topic The Substitution Method 2 Topic The Substitution Method California Standard 9 0 Students Solve A System Of Two Linear Equations Ppt Download



2x 3y 0 3x 4y 5



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions
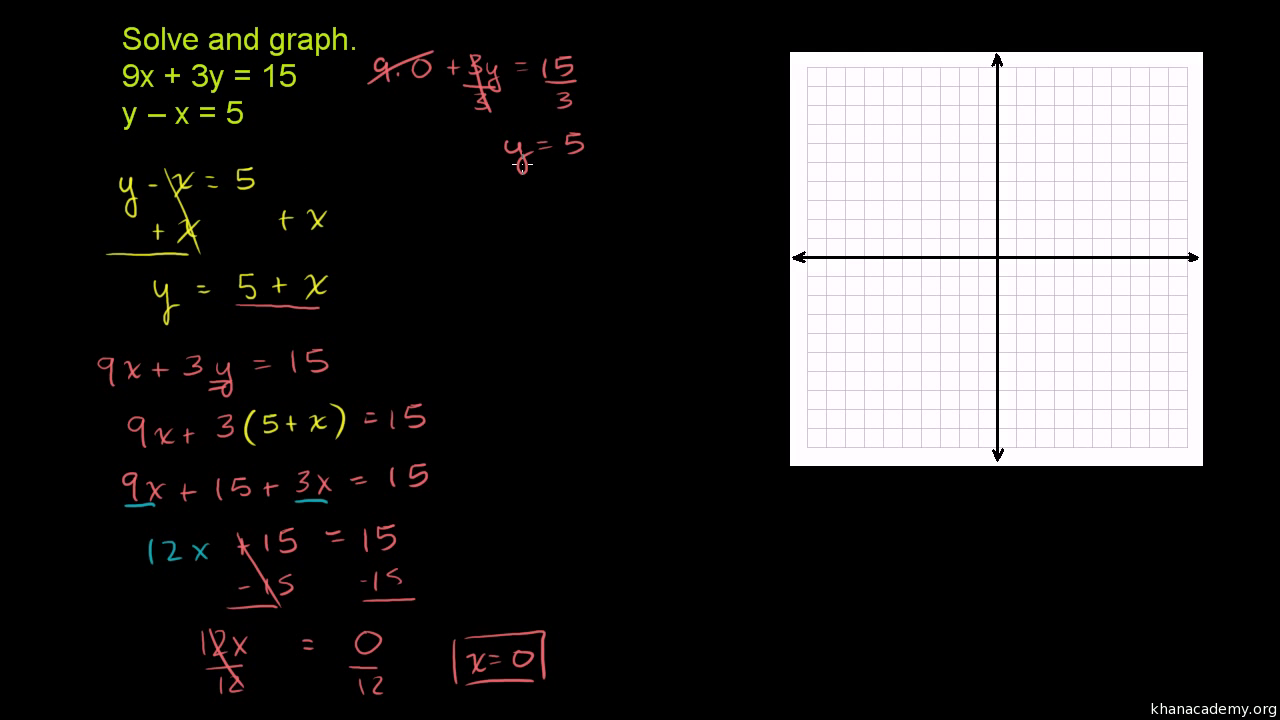



Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy



Systems Of Equations In Three Variables Boundless Algebra




J19




Q 1 2x 5y Xy 6 4x 5y Xy 3 Solve By Substitution Method Q 2 X 3 Y 4 11 5x 6 Y 3 7 0 Solve By Substitution Answer Fast Plz Maths Pair Of Linear Equations In Two Variables



2




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr



1



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline
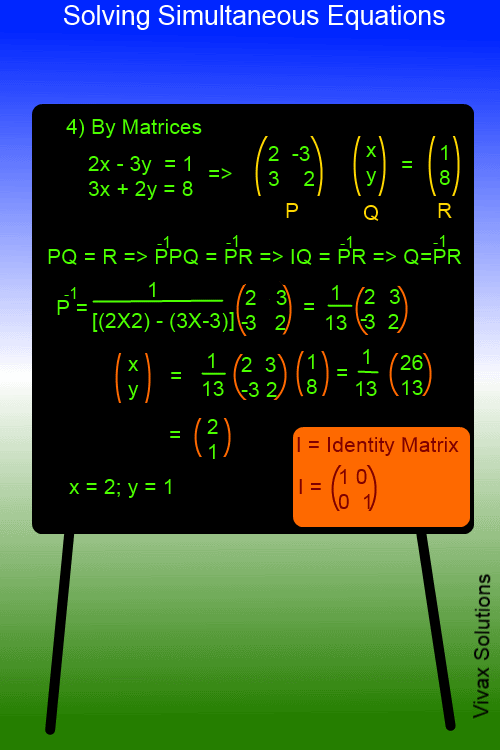



Solving Simultaneous Equations Elimination Substitution Graphical Matrix Methods Maths Tutorials Vivax Solutions



Simultaneous Equation Question The Student Room



3x 2 5y 3 2 X 3 Y 2 13 6
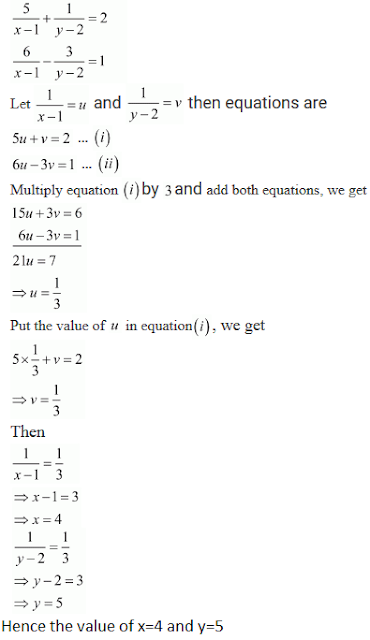



R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
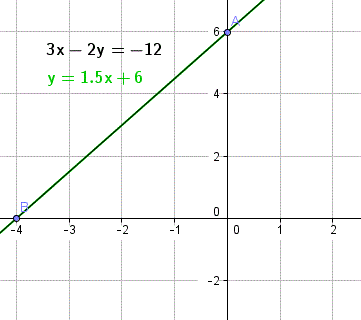



How To Solve Algebra




Systems Of Equations With Substitution Y 5x 8 10x 2y 2 Video Khan Academy




3 Systems Of Linear Equations
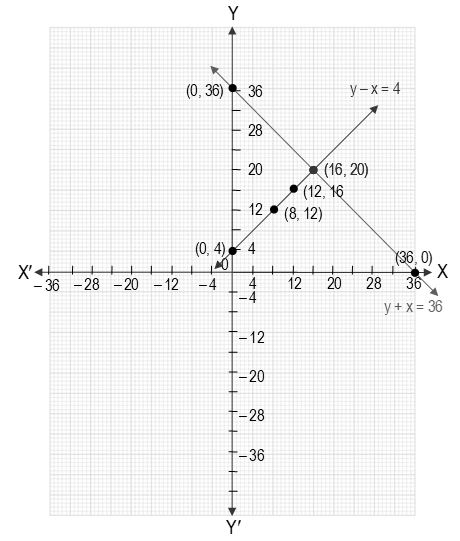



Pair Of Linear Equations In Two Variables



0 件のコメント:
コメントを投稿